Question
Using Lagrange multipliers, show that:
a) maximum value of ![]() subject to
subject to ![]() is
is ![]()
b) minimum value of ![]() subject to
subject to ![]() is
is ![]()
Solution
============================================================================================
a) maximum value of 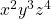 subject to
subject to 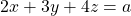 is
is 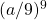
Objective function, ![]()
Constraint function, ![]()
Lagrange multiplier function: ![]()
Step-1: Find Gradient of f
![Rendered by QuickLaTeX.com \[ \nabla f(x_0,y_0,z_0) = \begin{bmatrix} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}\\ \frac{\partial f}{\partial z}\end{bmatrix} = \begin{bmatrix} 2xy^3z^4\\ 3y^2x^2z^4\\ 4z^3x^2y^3 \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-5b53a881d4d047a5a6b47f46a032b2c2_l3.png)
Step-2: Find Gradient of g
![Rendered by QuickLaTeX.com \[ \nabla g(x_0,y_0,z_0) = \begin{bmatrix} \frac{\partial g}{\partial x}\\ \frac{\partial g}{\partial y}\\ \frac{\partial g}{\partial z}\end{bmatrix} = \begin{bmatrix} 2\\ 3\\ 4 \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-3f4062a4ecddacc807134781132aa95b_l3.png)
Step-3: Find x, y and ![]()
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} 2xy^3z^4\\ 3y^2x^2z^4\\ 4z^3x^2y^3 \end{bmatrix} = \lambda_0 \begin{bmatrix} 2\\ 3\\ 4 \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-64e09e3aa5b494a03e59724e2d052303_l3.png)
![]()
![]()
Step-4: Substitute and figure out function values
Let’s take ![]() as the question is to prove maxima.
as the question is to prove maxima.
Let c = ![]() ,
,
Apply c in Constraint function ![]()
![]()
Apply (7) in (1) ![]()
![]()
Thus, f has maxima at ![]() . Hence, proved.
. Hence, proved.
============================================================================================
b) minimum value of 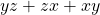 subject to
subject to 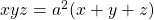 is
is 
Objective function, ![]()
Constraint function, ![]()
Lagrange multiplier function: ![]()
Step-1: Find Gradient of f
![Rendered by QuickLaTeX.com \[ \nabla f(x_0,y_0,z_0) = \begin{bmatrix} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}\\ \frac{\partial f}{\partial z}\end{bmatrix} = \begin{bmatrix} y+z\\ x+z\\ x+y \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-593f907a68523b63e11249c451b50c9c_l3.png)
Step-2: Find Gradient of g
![Rendered by QuickLaTeX.com \[ \nabla g(x_0,y_0,z_0) = \begin{bmatrix} \frac{\partial g}{\partial x}\\ \frac{\partial g}{\partial y}\\ \frac{\partial g}{\partial z}\end{bmatrix} = \begin{bmatrix} yz-a^2\\ xz-a^2\\ xy-a^2 \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-c740cd7c17b131f0cdf903cd2fb73158_l3.png)
Step-3: Find x, y and ![]()
![Rendered by QuickLaTeX.com \[ \Rightarrow \begin{bmatrix} y+z\\ x+z\\ x+y \end{bmatrix} = \lambda_0 \begin{bmatrix} yz-a^2\\ xz-a^2\\ xy-a^2 \end{bmatrix} \]](https://ehanghalib.com/wp-content/ql-cache/quicklatex.com-c1cc3cf2347a13c3fae04df196dfd3ee_l3.png)
(1) ![]()
Similarly, we get,
(2) ![]()
(3) ![]()
RHS of the equations (1), (2) and (3) are the same. Thus, let’s equate LHS of (1) = (2)
![]()
Similarly, (2)=(3) and (1)=(3) will give ![]() =1/x,
=1/x, ![]() =1/z
=1/z
Thus, x=y=z=![]()
Step-4: Substitute ![]() and figure out function values
and figure out function values
Apply ![]() in Constraint function
in Constraint function ![]()
Let ![]()
![]()
Let’s take ![]() as the question is about a minima.
as the question is about a minima.
Apply ![]() in Objective function
in Objective function ![]()
![]()
Thus, f has minima at ![]() . Hence, proved.
. Hence, proved.