Let $A_{m \times n}$ be a given matrix with $m > n$. If the time taken to compute the determinant of a square matrix

Question

Let $A_{m \times n}$ be a given matrix with $m > n$ . If the time taken to compute the determinant of a square matrix of size j is $j^3$ , find upper bound on the total time taken to find the rank of A using determinants.

Solution

This problem has multiple parts. So dividing the solution attempt into the respective steps that posed a challenge to me.

Part 1: Method to find rank of a matrix using determinants

Theory:

Basically, we need to check if there is at least one non-zero determinant for a given order of square submatrices. An order of 2 means square submatrices of size $2 \times 2$ . We need to check the same for orders $1,2,3,..$ etc. If for a given order k, there are no square submatrices with a non-zero determinant, then the rank of the matrix is $k - 1$ .

In-Context:

Since we need to find the upper bound for the given matrix $A_{m \times n}$ & $m > n$ , the orders till n has to be checked.

Part 2: Formula of time taken to find determinant of one square submatrix of order n

Size of a square matrix of order $2 = 2^2$
Size of a square matrix of order $3 = 3^2$
Therefore, Size of a square matrix of order $n = n^2$

Let time taken to find determinant of submatrix for a given size be $t_{size}$ ,
For size $j, \emsp t_j = j^3$

(1) $\begin{equation*} \begin{minipage}{0.8\textwidth} Therefore, time taken to find determinant of one square submatrix of order $n = (n^2)^3$ \end{minipage} \end{equation*}$

Part 3: Finding number of square submatrices of order k for a matrix of size 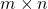$m \times n$

No. of submatrices of size $a \times b$ for a matrix $m \times n = (m-a+1)(n-b+1)$
In the case of square submatrices, $a = b = k$

(2) $\begin{equation*} \begin{minipage}{0.8\textwidth} No. of square submatrices of size $k \times k$ for a matrix $m \times n = (m-k+1)(n-k+1) \end{minipage} \end{equation*}$

Part 4: Total time taken to find the rank of A using determinants

Total time to find the determinants for a given order $= Eq.(1) * Eq.(2)$

For every order k, we will need to multiply (1) and (2) to find time taken for that order. To find time taken for all n orders, the individual products (1) * (2) of every order will have to be summed up.

I.e. for nth order, $t_{n \times n} = (n^2)^3⋅[(m-n+1).(n-n+1)]$

Thus, applying summation, total time to find the rank of A using determinants

(3) $\begin{equation*} \left t_{m \times n} = \sum_{k=1}^{n}{(k^2)^3.[(m-k+1).(n-k+1)]} \end{equation*}$

Part 5: Finding the Upper Bound for total time taken to find the rank of A using determinants

Expanding (3),

(4) $\begin{equation*} \left t_{m \times n} = \sum_{k=1}^{n}{(k^5)[k^2 - k(m+n+2) + (mn+m+n-1)]} \end{equation*}$

In (4), the terms m & n are constants. Hence, let

$\begin{align*} \left c=m+n+2 \end{align*}$

$\begin{align*} \left d=mn+m+n-1 \end{align*}$

Apply c & d in (4),

$\begin{align*} \left t_{m \times n} = \sum_{k=1}^{n}{(k^5)[k^2 - c.k + d]} \end{align*}$

(5) $\begin{equation*} \left t_{m \times n} = \sum_{k=1}^{n}{(k^7) - c.k^6 + d.k^5} \end{equation*}$

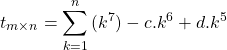
General summation formulae pattern:

$\begin{align*} \left 1 + 2 + 3 +...+ n = [n(n+1)]/2 \end{align*}$

$\begin{align*} \left 1^2 + 2^2 +...+ n^2 = [n(n+1)(2n+1)]/6 \end{align*}$

$\begin{align*} \left 1^3 + 2^3 +...+n^3 = [(n(n+1))/2]^2 \end{align*}$

$\begin{align*} \left 1^4 + 2^4 +...+ n^4 = [n(n+1)(2n+1)(3n2+3n-1)]/30 \end{align*}$

Inference >> From general summation formulae, I infer that for every order, the highest power in the formula will increase by 1.

Using the inference & ignoring the lower powers of the resultant polynomial equation, upper bound of (5) becomes,

$\begin{align*} \left T(n) \leq O(n^8) \end{align*}$

Thus, the upper bound for the polynomial equation that represents the total time taken to find the rank of A using determinants is of the order 8.

References:

1) Theory for finding rank using determinants.

2) Proof & formula for finding number of submatrices for a given matrix of size $m \times n$