Find the minimum distance from (4,2) to the parabola $y^2 = 8x$

Question

Solution

Conceptually, this can be done by:
1) Considering the curve and finding the tangent.
2) Find normal to that general tangent.
3) Solve the normal line equation by substituting (4,2) as its solution to get the point of tangent on curve.
4) Finding distance between the point of tangent on curve and given point (4,2).

Part-1: Find tangent to 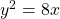$y^2 = 8x$

Let $y^2 = 8x = f$

(1) $\begin{equation*} \left\ \Rightarrow y = 2 \sqrt{2x} \end{equation*}$

As per point-slope equation forms, tangent is

(2) $\begin{equation*} \left\ y - y_0 = m(x - x_0) \end{equation*}$

(3) $\begin{equation*} \left\ f(x_0) = f'(x_0)(x - x_0) \end{equation*}$

(4) $\begin{equation*} \left\ y = (dy/dx)(x - x_0) + f(x_0) \end{equation*}$

(2), (3) & (4) are equations of tangent. (m = slope)

Part-2: Normal Line Equation

Equations of normal to tangent are:

(5) $\begin{equation*} y - f(x_0) = n(x - x_0) = (-1/m)(x - x_0) = (-1/f(x_0))(x - x_0) \end{equation*}$

$Here, m = dy/dx = (2/x)^{1/2}.$

$Thus, n = (-1/m) = -(x/2)^{1/2}$

(6) $\begin{equation*} (5) \Rightarrow y = (-(x/2)^{1/2}).(x - x_0) + 2 \sqrt{2x_0} \end{equation*}$

In (6), $(x_0, y_0)$ is the point on the curve and (x, y) denotes any point on the line.

Part-3: Solve the Normal Line Equation

We know that (4,2) must be on normal. Thus (x,y) = (4,2)

$\begin{align*} \left 2 = -(2/\sqrt{2})(4 - x_0) + 2 \sqrt{2x_0} \\ 2 = -(\sqrt{2})(4 - x_0) + 2 \sqrt{2x_0} \\ = \sqrt{2} - 4 \sqrt{2} + 2 \sqrt{2x_0} \\ 2 + 4 \sqrt{2} = x_0(\sqrt{2} + 2 \sqrt{2}) \\ \Rightarrow x_0 = 1.8 \\ \Rightarrow y_0 = 2 \sqrt{2x_0} = 3.8 \end{align*}$

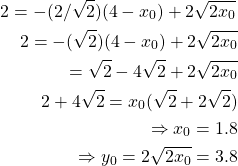
Thus, the point on curve closest to (4,2) is (1.8,3.8)

Part-4: Find the distance between (4,2) & (1.8,3.8)

Equation to find distance between 2 points on a plane

$\begin{align*} \boxed{ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} } \\ d = \sqrt{(4 - 1.8)^2 + (2 - 3.8)^2} \\ = \sqrt{4.84 + 3.24} = \sqrt{8.08} \approx 2 \sqrt{2} \end{align*}$

Thus, the minimum distance from (4,2) to the parabola $y^2 = 8x$ is $2 \sqrt{2}$